大学受験化学を攻略しよう

2019年　神戸大学　化学　解説

【問題分析】

2019年の神戸大学の化学の問題は、2018年の問題に引き続き、基礎的なことがしっかりとできていればほとんどの問題に解答することができます。

【解答上のポイント】

Ⅰは無機化学系の基本問題です。
問1は無機化学、問2, 3, 4は結晶、問5, 6は化学反応とエネルギーです。

問1で注意すべき点は、白金を溶かす王水について、その作製方法を答える問題で濃硝酸と濃塩酸と答えるところでしょうか。
単なる塩酸と硝酸では×です。

問2, 3の結晶の問題では面心立方格子とダイヤモンド型の結晶構造が問われました。
よくある典型問題で単位格子の中に原子が何個あるかを答える問題でした。
面心立方格子は結晶構造が描いていないので覚えておかなければなりません。注意点として、面心立方格子の中心には原子はありません。
ダイヤモンド型構造で気を付ける点は単位格子の中に完全に含まれている原子が4個あるということです。後は角と面の原子を合わせて全部で8個です。

問5の問題について、触媒が変化させるのは、反応経路、活性化エネルギー、反応速度です。

【解答上のポイント】

Ⅱは溶液の平衡に関する問題です。
平衡の問題は入試の定番で、問題によっては非常に難しい問題が出題されることもありますが、 Ⅱの問題は非常に簡単な問題設定なので全問正解したいです。
問1と問3は知識問題、問2は平衡の計算問題です。

問1はリンに関する知識問題です。ア～エの問題は定番の問題です。 特殊な問題はないので、すべて正解できなければなりません。
あえて注意すべき問は「イ」でしょうか。黄リンは空気中で自然発火するので水中に保存します。
Na等を石油中に保存するのと混同しないようにしましょう。
リンは無極性分子なので石油に入れると溶けてしまうため水の中に保存します。

問2は平衡の計算問題です。





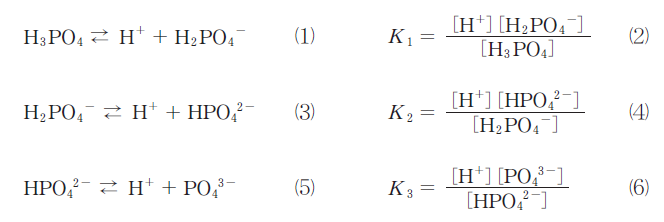
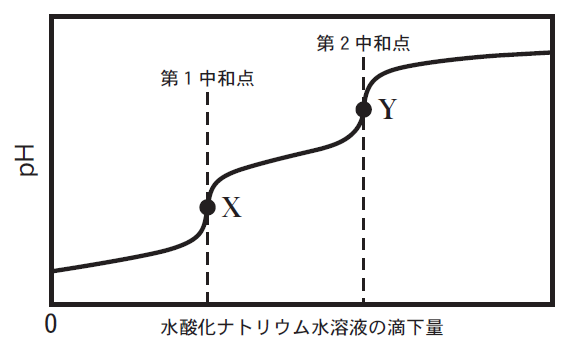
「A」と「C」はそれぞれH₃PO₄の1個のH、H₂PO₄^- の1個のHと反応するOH^-の数になります。
従って点Xまでに加えるNaOHのモル数はH₃PO₄のモル数と同じになります。実際にはmLを計算して答えることになります。 初めに存在したH₃PO₄も、Hを1個だけ中和してできたH₂PO₄^-も同じモル数なので、 「A」と「C」は同じモル数＝体積になります。

「B」に関しては(8)式が問題文に書いてあるので簡単に計算できます。もし(8)式が与えられていなければ、 自分で導出しなければならないので少し難しくなります。ということで、この問題は親切な設定になっています。

pH = -log₁₀[H⁺]なので

\(\displaystyle [H^{+}]^{2} = K_{1}K_{2}\)　　　　　(8)

から

\(\displaystyle \ log_{10} [H^{+}]^{2} = \log_{10} K_{1}K_{2}\)

\(\displaystyle \ 2 log_{10} [H^{+}] = \log_{10} K_{1} + \log_{10} K_{2}\)

\(\displaystyle \ -log_{10} [H^{+}] = -\frac{\log_{10} K_{1} + \log_{10} K_{2}}{2}\)

\(\displaystyle\log_{10} K_{1}=-2.1, \log_{10} K_{2}=-7.2\)　なので

\(\displaystyle \ -log_{10} [H^{+}] = -\frac{-2.1 + -7.2}{2}=4.65\fallingdotseq 4.7\)　←Bの答え

となります。

「D」から複雑になります。
まず前提として基本的にナトリウム塩は水に溶けると完全に電離します。
したがって、Na₂HPO₄1molからHPO₄^2-が1mol、 NaH₂PO₄1molからH₂PO₄^-が1molできます。
これを前提に、0.10 mol/L のリン酸水素二ナトリウム（Na₂HPO₄）水溶液10 mL と 0.10 mol/Lのリン酸二水素ナトリウム（NaH₂PO₄）水溶液10 mL を混合し， 純水で100 mL に希釈したときのHPO₄^2-とH₂PO₄^-の濃度を求めます。

HPO₄^2-のモル数は

\(\displaystyle \ 0.10 \times \frac{10}{1000}=1.0 \times 10^{-3} \) mol

これが100 ｍLに入っているので、濃度は

\(\displaystyle \ 1.0 \times 10^{-3} \times \frac{1000}{100}=1.0 \times 10^{-2}\) mol/L

同様にしてH₂PO₄^-の濃度は\(\displaystyle \ 1.0 \times 10^{-2}\) mol/Lとなります。

(3)式　（H₂PO₄^-　⇄　H⁺ + HPO₄^2-）　の平衡のみ考えると電離定数は

\(\displaystyle \ \frac{[H^{+}][HPO_{4} \, ^{2-}]}{[H_{2}PO_{4} \, ^{-}]}\)

となります。

ここで大ざっぱな見積もりで計算します。
問題の設定では水の電離を無視できると書いてあるので、[H⁺]の初期値は0です。
(3)式の平衡が少し右に移動し、[H⁺]が生成したとします。
K₂の値は非常に小さく、6.3×10^-8なので、H₂PO₄^- がほんの少しだけ電離して[H⁺]が6.3×10^-8mol/L生成したとすると

\(\displaystyle \ \frac{[H^{+}][HPO_{4} \, ^{2-}]}{[H_{2}PO_{4} \, ^{-}]}=6.3 \times 10^{-8} = K_{2}\)　　　(a)

になります。
[H⁺]が6.3×10^-8mol/L生成するとき、H₂PO₄^-が6.3×10^-8mol/L減少し、 HPO₄^2-が6.3×10^-8mol/L生成します。
ところが、H₂PO₄^-とHPO₄^2-の初期値1.0×10^-2mol/Lに対して変化量 6.3×10^-8mol/Lは非常に小さいため

　HPO₄^2- ： 1.0×10^-2 + 6.3×10^-8 ≒ 1.0×10^-2
　H₂PO₄^- ： 1.0×10^-2 - 6.3×10^-8 ≒ 1.0×10^-2

となり、計算する上でHPO₄^2-とH₂PO₄^-の増減は無視することができるため、 [HPO₄^2-] = [H₂PO₄^-] となります。
この時(a)式は

\(\displaystyle \ [H^{+}]=6.3 \times 10^{-8} = K_{2} \)

となります。

pH = -log₁₀[H⁺]なので(a)式の両辺対数をとり、さらに\(\displaystyle \log_{10} K_{2}=-7.2\)　なので

pH =\(\displaystyle \ -log_{10} [H^{+}] = - \log_{10} K_{2}\)=7.2　←Dの答え

となります。

このような大ざっぱな計算方法では納得いかないとなると次のように、H₂PO₄^-が反応した濃度をαとして反応前後の濃度を計算し、方程式を立てるしかありません。



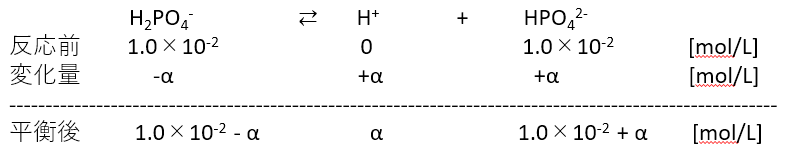
このとき(a)式は

\(\displaystyle \ \frac{\alpha \times (1.0 \times 10^{-2} + \alpha)}{1.0 \times 10^{-2} - \alpha} = 6.3 \times 10^{-8} \)

\(\displaystyle \ \alpha ^{2} + (1.0 \times 10^{-2} + 6.3 \times 10^{-8})\alpha - 6.3 \times 10^{-10} = 0 \)

この式において、

\(\displaystyle \ (1.0 \times 10^{-2} + 6.3 \times 10^{-8})\alpha \fallingdotseq 1.0 \times 10^{-2}\alpha \)

と近似し、この二次方程式を解くと

\(\displaystyle \ \alpha =-1.0 \times 10^{-2}, \, 6.29996 \times 10^{-8} \)

となるので

\(\displaystyle \ \alpha =6.3 \times 10^{-8} \)

としてよいことがわかります。結論をいうと厳密に方程式を解いたとしても、大ざっぱな見積もり計算とほとんど変わりません。

「G」はHPO₄^2-とH₂PO₄^-の比が1:1の液に強酸であるHClを入れたとき、pHはどうなるか、という問題です。
リン酸は緩衝液、すなわち少量の酸やアルカリを加えてもpHはほとんど変化しない溶液なので、「D」の値と同じような答えが予想されます。
問題文の中に「あまり変化しない」と書いてあるので本問の場合はいいですが、もしpHの変化について書かれていなかったとしても、答えを予想することは必要です。
もし全然違う値になれば計算が間違っているかもしれないと気付くことができるかもしれません。
もちろん大量にHClを加えると緩衝機能が働かなくなり、pHは大きく変化します。

HClを入れたときの反応式として(9)式が与えられています。
この式によればHPO₄^2-とH⁺は不可逆的に反応して、H₂PO₄^-が生成することがわかります。

HPO₄^2- + HCl　→　H₂PO₄^- + Cl^-　　　　　(9)

HPO₄^2-よりもHClの方が量が少ないので、加えたHClはすべて反応し、未反応のHPO₄^2-が残ります。
これを丁寧に書いて計算すると次のようになります。



したがって、HPO₄^2-が0.80×10^-2、H₂PO₄^-が1.2×10^-2mol/Lになります。
ここからは「D」を求めたときと考え方は同じです。今回は[HPO₄^2-]/[H₂PO₄^-]=2/3 になっただけです。
「D」では[HPO₄^2-]/[H₂PO₄^-]=1だったのが2/3になったときどうなるかですが、 (4)式の両辺が等しくなるためには[H⁺]は「D」の時の3/2倍になればよいことがわかります。
6.3×10^-8が3/2倍になっても平衡を満たすために反応する[HPO₄^2-]も[H₂PO₄^-]の濃度も元の濃度に比べて5～6桁小さいので計算上は無視することができます。

\(\displaystyle \ \frac{[H^{+}][HPO_{4} \, ^{2-}]}{[H_{2}PO_{4} \, ^{-}]} = K_{2} = 6.3 \times 10^{-8}\)　　　　　　(4)

式(4)から

\(\displaystyle \ [H^{+}]= \frac{[H_{2}PO_{4} \, ^{-}]}{[HPO_{4} \, ^{2-}]} \times K_{2} = \frac{3}{2} \times K_{2}\)

H = -log₁₀[H⁺]なので上式の両辺対数をとり、さらに\(\displaystyle \log_{10} K_{2}=-7.2, \, \log_{10} 2.0=0.30, \, \log_{10} 3.0=0.48\)　なので
pH =\(\displaystyle \ -log_{10} [H^{+}] = - (\log_{10} 3.0 + \log_{10} K_{2}-\log_{10} 3.0) = - (0.48 -7.2 -0.30) =7.02 \fallingdotseq 7.0\)　　←Gの答え

となります。
計算するとき、K₂の値6.3×10^-8を入れて計算してしまうと、logの計算できなくなってしまうので注意が必要です。

【解答上のポイント】

Ⅲは有機化学の構造決定の問題です。
構造決定といっても半分は基本的な知識問題です。
問題3,5が条件から構造を推測する構造決定問題です。構造決定問題を早く、正確に解答するためには基本的な反応をよく覚えておくことです。

問1
ヨードホルム反応の問題です。
黄色の沈殿はヨードホルム、分子式はCHI₃です。

問2
問題文によると化合物Cはベンゼンとプロペンから合成できるものです。
これが何かというとクメン法でフェノールを合成するときの中間物質のクメンです。



問題文中の「化合物Cを酸素で酸化したのち、硫酸で分解すると化合物Gと化合物Hが生成した」も正に上記の反応式の説明です。
問題文の後の説明から化合物Gはフェノールで化合物Hはアセトンです。
ちなみに、クメンを酸化してできるクメンヒドロペルオキシドのペルオキシド（英: peroxide）とは過酸化物の意味です。この化合物では-O-O-結合があるため過酸化物となります。

「化合物H（アセトン）は化合物Jの乾留によって得られる」とあります。
ここまでくれば単なる知識問題です。化合物Jは酢酸カルシウムです。
化合物J（酢酸カルシウム）を乾留をすると下記の式に従い、化合物H（アセトン）が生成します。

Ca(CH₃COO)₂ → CH₃COCH₃ + CaCO₃

問3、5
化合物Iの構造式を答える問題は単なる知識問題です。
化合物G（フェノール）と臭素が反応してできるのは2,4,6-トリブロモフェノールです。


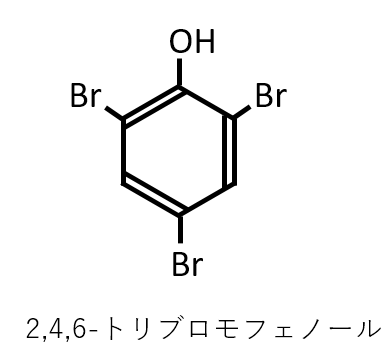
Ⅲの中では化合物Dと化合物Aを決める問題のみが一般的な構造決定問題です。
問題では化合物D先に聞かれていますが、化合物A（問5）から決定した方がやりやすいので、化合物Aから決めていきました。

問題文(a)によると化合物Aは分子式がC₉H₁₂Oでベンゼン環を持つ化合物であり、2種類の構造異性体が存在する、と書いてあります。
ここで注意するのは構造異性体といってもこの場合いろいろ制約があり、純粋にC₉H₁₂Oの構造異性体のことを言っているのではないということです。
構造異性体というのは分子式が同じで原子の結合順序が異なるもののことです。
制約を考えないと分子式C₉H₁₂Oの構造異性体は相当な数あります。

分子式C₉H₁₂Oで表される化合物Aの構造異性体の制約は、
　1. ベンゼン環を持つ
　2. 化合物Aは濃硫酸と反応する
　3. 濃硫酸と反応してできた化合物Bは水素が付加する
　4. 化合物Bに水素が付加してできた化合物はクメンである

ベンゼン環を持ち、反応するとクメンができるので、化合物Aのベンゼン環と炭素の骨格を描くと次のような構造になります。


次に濃硫酸と反応する、反応後の化合物は水素が付加する、ということから、濃硫酸による脱水反応により、 元の化合物には二重結合ができると考えると化合物Aは下記の2種類となります。
また、これが問5の答えです。


すなわち、-OH基が端の炭素原子に結合したものと、真ん中の炭素原子に結合したものが考えられ、 どちらの構造でも硫酸による脱水反応でC=C結合をもつ化合物Bが1種類生成します。

化合物Bは次のような構造です。



さらに反応を見ていきます。
　1. 問題文(c)によると化合物Bはオゾン（O₃）と反応して化合物Dと化合物Eが生成する
　2. 問題文(d)によると化合物Dはヨードホルム反応する
となっています。

化合物Bに二重結合がある、オゾンと反応する、ということから次のオゾン分解が起こると考えられます。



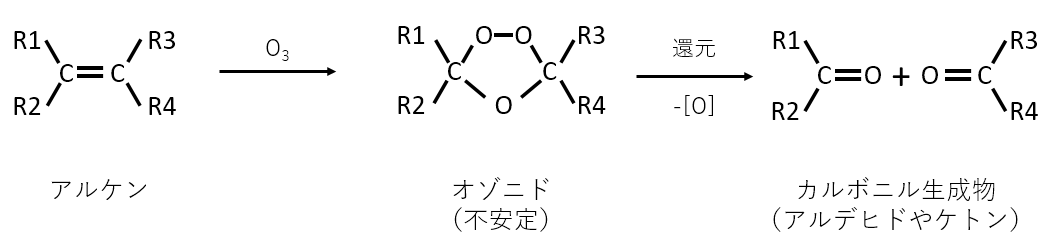
オゾン酸化により2つの化合物ができますが、化合物Dはヨードホルム反応するということから、化合物Dは次のような構造になります。
これが問3の答えです。



尚、化合物EはHCHOで表されるホルムアルデヒドです。

問4
問4は知識問題です。
フェノール（化合物G）と塩化ベンゼンジアゾニウムが反応してできる赤橙色の化合物は、p-ヒドロキシアゾベンゼン（p-フェニルアゾフェノール）です。
反応名は「カップリング」です。正確に覚えておきましょう。
この反応は教科書にも載っていますので特別な問題ではありません。わからなければ勉強不足ですので知識を増やすようにしてください。

----↑　Ⅲ　----

----↓　Ⅳ　----

【解答上のポイント】

Ⅳはタンパク質の問題です。
どれも基本的な知識を知っているかどうかを試す問題です。

ビウレット反応に使う水溶液やフェーリング液の銅に関する問題が出題されました。
ビウレット反応に使うのは硫酸銅（Ⅱ）水溶液です。
また、フェーリング液とは、硫酸銅（Ⅱ）、酒石酸カリウムナトリウム（ロッシェル塩）、水酸化ナトリウム（水酸化カリウム）を混合した水溶液です。
従って、ビウレット反応で使う液に含まれている金属イオンを答える問3はCu²⁺になります。

フェーリング反応で生成する赤色沈殿はCu₂O（問6）です。これは、アルデヒド基によりCu²⁺が還元されたことにより、銅の価数が1価の酸化物ができるためです。
一方で、ビウレット反応はCu²⁺がトリペプチド以上のペプチドと錯体を形成することにより発色する反応です。
同じ銅を使用していても反応の機構は全く異なります。

本問のように、共通している銅に関して問われるような問題形式の場合、よく覚えておかないと、例えば問3で金属イオン（銅イオン）がCu²⁺かCu⁺か、 また問6の赤色沈殿がCu₂OかCuOで迷うことになります。
ほんの少しのことで問題の難易度が上がっているように思います。

----↑　Ⅳ　----


＜終わり＞