大学受験化学を攻略しよう

2018年　神戸大学　化学　解説

【問題分析】

2018年の神戸大学の化学の問題は、基礎的なことがしっかりとできていればほとんどの問題に解答することができます。

【解答上のポイント】

【一問一答】

【解答上のポイント】

Ⅱはモール法に関する問題です。モール法は溶解度積の応用で、入試問題の定番です。
モール法はさらっと問題を解くだけなら簡単ですが、深く考えると非常に複雑です。
よく理解していないと、少し詳しいことを問われてしまうと解答できなくなります。

問1、問2は銀イオンに関する知識問題です。

問3はモール法に関連した計算問題です。一部の問題は問題文の内容がわかりにくいと思いました。
④、⑤に関しては、
問題文中の
「さらにA液にB液を滴下しつづけるとにごりが増していった。B液を13.5mL滴下したときに うすい暗赤色のAg₂CrO₄の沈殿が生成し、かくはんしても沈殿の色が変わらなかったため、これを終点とした。」
から、加えたAg⁺がCl^-と反応してAgClができたとすると、液中に存在したCl^-の物質量は、加えたAg⁺と同量なので
\(\displaystyle 5.00 \times 10^{-2} \times \frac{13.5}{1000}=6.75 \times 10^{-4} \) mol
と求めることができます。

単に計算するだけなら簡単ですが、なぜこれで滴定の実験が成立しているといえるかを検証する考察がこの後の文章に続きます。

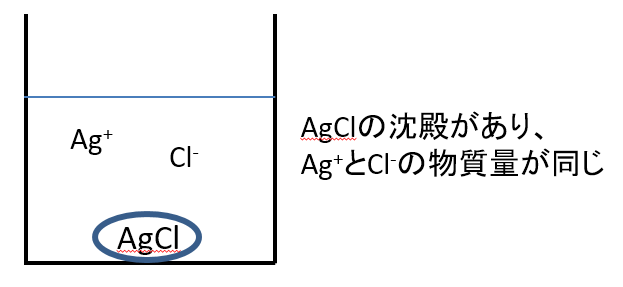
「A液15.0mL中のCl^-の物質量とAg⁺の全物質量が等しくなるようにB液を滴下したとき」とういうところがわかりにくいですが、 A液とB液を混合することにより、下の図のようにAgClの沈殿が生じた状態で尚且つ液中のAg⁺とCl^-の物質量が等しい状態をこの文章が表しているとします。するとこのとき、 沈殿と液中を合計したAg原子の全物質量とCl原子の全物質量は等しいことになります。
尚、この時液中に存在したCl^-に対してちょうど同じ量のAg⁺を加えた点なので理想的な滴定の終点です。しかし滴定中にこの理想的な終点を知るすべはありません。



なぜ、液中のAg⁺とCl^-の物質量が等しい時、沈殿と液中を合計したAg原子の全物質量とCl原子の全物質量が等しいかという理由の考え方を2つのパターン（考え方1、2）で示します。
どちらもほとんど同じようなことをいっていますが理解しやすいほうで考えてください。
考え方1
一度、液中のAg⁺とCl^-が反応してすべてAgClになり、液中にはAg⁺とCl^-が存在しない状態を仮定します。 その後AgClが少し溶けたとすると、1個のAgClから同数のAg⁺とCl^-ができるため、液中には等しい物質量のAg⁺とCl^-が存在するようになります。
言い換えるとビーカーの中のAgとClの物質量が等しくないと、液中のAg⁺とCl^-の物質量は等しくなりません。

考え方2
沈殿のAgClの中のAgとClの物質量は同じです。するとビーカーの中全体でAgとClの物質量が等しくなるためには液中のAg⁺とCl^-の物質量が等しい必要があります。

AgClの溶解度積は\(\displaystyle [Ag^{+}][Cl^{-}]=1.80 \times 10^{-10}\) で、液中のAg⁺とCl^-の物質量が等しい時\(\displaystyle [Ag^{+}]=[Cl^{-}]\) なので \(\displaystyle [Cl^{-}]^{2}=1.80 \times 10^{-10}\) となり、問題文の冒頭で\(\displaystyle \sqrt{1.80}= 1.34\)と与えられているので\(\displaystyle [Cl^{-}]=1.34 \times 10^{-5}\)mol/Lとなります。これが④と⑤の答えです。

⑥は、
A液15.0mLにB液13.5mLを加えた後のCrO₄^2-の濃度が\(\displaystyle [CrO_4\,^{2-}]=2.85 \times 10^{-4} \times \frac{1000}{15.0+13.5}=1.00 \times 10^{-2} \) mol
のため、
\(\displaystyle [Ag^{+}]^{2}[CrO_4\,^{2-}]=4.00 \times 10^{-12}\)
から、Ag₂CrO₄の沈殿が生成する最も低いAg⁺の濃度は
\(\displaystyle [Ag^{+}]^{2}=\frac{ 4.00 \times 10^{-12}}{1.00 \times 10^{-2}}=4.00 \times 10^{-10}\)
\(\displaystyle [Ag^{+}]=2.00 \times 10^{-5}\)mol/L
となります。
⑥の値2.00×10^-5は⑤の値1.34×10^-5よりも少し大きいので、Ag⁺とCl^-の物質量が等しくなったすぐ後にAg₂CrO₄の暗赤色の沈殿ができるため、滴定の終点を知ることができるという訳です。
正確にいうと少しだけ多くAgを加えなければならないのでその分が誤差となります。
もし⑤と⑥の値が逆であれば、Clがすべて反応してしまう前にAg₂CrO₄の沈殿が生成し始めてしまうのでClの量を少なく評価してしまいます。

【注意点】
このタイプの問題は液量が変化するために、濃度の計算には注意が必要です。求めようとしている時の液量がいくらなのかに注意する必要があります。
逆にいうと、問題が複雑になり、受験生が間違いやすそうな問題になるので差をつけるために出題したくなるのでしょう

【補足】
本問題には出てきませんが、モール法で他によく問われる問題は何かわかりますか。
それは、滴定は中性で行わなければならないということです。
酸性が強いと、CrO₄^2-がCr₂O₇^2-に変化し、指示薬の役割ができない、
塩基性が強いとAg⁺がOH^-と反応してAg₂Oに変化し、滴下したAg⁺がCl^-との反応以外に使われてしまう、ためです。
問題は解くだけではなく、自分で問題を作ることができるようになると成績もどんどん上がります。

私は実際にはモール法の実験をしたことはありません。ここまで見てきたようにモール法は非常に難しい実験だと思います。
滴定するときはそもそもCl^-の濃度は未知です。
問題ではうまく滴定できるように数値が設定されていますが、濃度が未知のCl^-を滴定するためには指示薬として添加するK₂CrO₄の濃度をいくらにすればよいか分かりません。
濃度が高すぎると滴定の終点となるべき点よりも前にAg₂CrO₄が生成して色が付きますし、薄すぎると滴定の終点となっても色が付かず、色が付くまで加えたAgが大きな誤差になります。
正しく滴定するためには条件を変えて何度もやり直す必要がありそうです。

【解答上のポイント】

Ⅲは有機化合物の構造決定の問題です。
分子式はC₅H₁₀Oで、問題文には構造異性体として化合物群が4つでてきます。
いくつか分類が出てくるので問題文を読みながら、下の図のように条件を簡単にメモしておくと解答しやすいと思います。



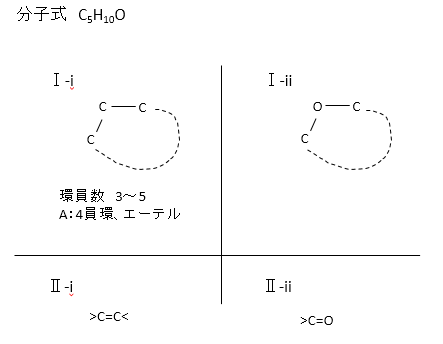
分子式から不飽和度は1とわかるので二重結合が1つまたは環状構造が1つあることがわかります。
二重結合として考えられるのはC=CとC=Oです。
本問の場合、C=Oから考えられる構造はケトン（R-CO-R'）かアルデヒド（-CHO）です。
分子式にはOが1つしかないのでエステル結合（-COO-）やカルボキシ基（-COOH）はありません。
本問において、Oが二重結合を作らない構造はエーテル結合（-O-）かヒドロキシ基（-OH）です。
従って、問題文の「化合物群（Ⅰ-i）において可能な環員数は3～5だが、分子式を考慮すると、これらはエーテルまたは「ア」と考えられる」 の「ア」の答えはアルコールです（アルコールはヒドロキシ基がある）。
わからなくても文脈から推定できると思いますが、問題文に出てくる「環員数」とは環を構成する原子の数です。
また問題文に出てくるエーテルとはR-O-R'の構造で、鎖状構造だけでなく、環状構造の中にあってもエーテルです。

【一問一答】

【解答上のポイント】

Ⅳは高分子系の問題です。
出題内容は頻出事項ですが、問1の穴埋め問題は語句を記入する前後に鍵となる言葉が抜けていたり、 問3、4もヒントが少ないので相当勉強していないと解答しづらかったのではないでしょうか。
例えば、「ウ」の後ろに「結合」、「エ」の後ろに「構造」という語が入っていれば答えやすかったかもしれませんが、 少しの違いで分かりにくくなっていると思います。
問3、4に関しては、ポリビニルアルコールの問題を暗記するぐらいやっていれば簡単に解けたと思います。
この問題は下記のように繰り返しの最小単位の2個を一組にして考えるのがポイントです。
この図がすぐに浮かばなければ、問3、4に解答するのは困難です。



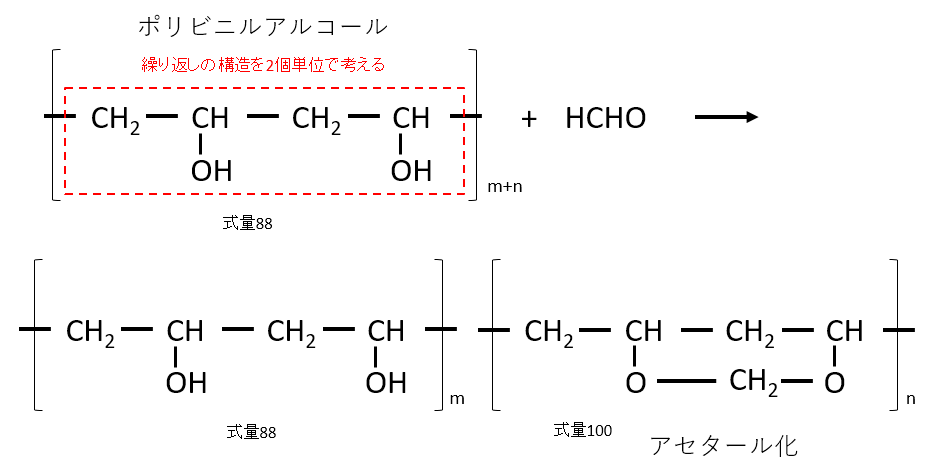
問4
計算方法は次のようになります。

重量変化は、

\(\displaystyle \frac{\{88m+100n\}-\{ 88(m+n)\}}{88(m+n)} \times 100 = \frac{12n}{88(m+n)} \times 100\)

40%のヒドロキシ基が反応したので、

\(\displaystyle \frac{n}{m+n} \times 100 = 40\)

従って、

\(\displaystyle \frac{12n}{88(m+n)} \times 100=\frac{12}{88}\times 40=5.454\)

となるので答えは5.45%です。